Think more clearly by reducing bias
Improve judgement and logical thinking by understanding cognitive biases
“What one book would you recommend to students, new grads and early career folks?”
I’ve been asked this question many times.
My answer? Thinking, Fast and Slow by Daniel Kahneman.
Thinking, Fast and Slow introduced me to the world of clear thinking, decision-making, and mental models. It’s worth a proper read (vs. skimming or reading a summary).
The TL;DR is that we rely on two systems of thinking:
System 1 (Thinking Fast) is the intuitive, subconscious “gut response” way of thinking and decision making. It’s always-on and gives us the ability to create fast impressions, judgements, and intuition.
System 2 (Thinking Slow) is the analytical, logical, intentional way of decision making. It’s used for reflection, analysis, and problem solving.
Most of the time, we engage System 1. Which may lead to biased decision making and poorer choices. It’s also easier to use System 1 as it requires much less cognitive effort.
We have a limited amount of daily cognitive power to use. Each decision we make taxes our brain and the quality of our decisions begins to erode over the course of a typical day.
Steve Jobs famously wore the same outfit every day so he never had to think about what to wear.
Barack Obama replies to his low priority emails to "Agree, "Disagree" or "Discuss" to simplify his workflow.
Decision fatigue is real and as we consume our mental resources, we subconsciously rely on passive heuristics (mental shortcuts) to make decisions. That's why it's important to regularly sharpen our mental models.
Acknowledging the cognitive biases that affect our thinking allows us to stay rational. It only takes a second to ask ourselves "What am I missing here?" or "What irrational factors may be influencing my judgement?".
Here are 8 cognitive biases you should know about:
👍🏽 Confirmation Bias
People are prone to believe what they want to believe. Confirmation bias is the tendency to subconsciously seek information to validate existing beliefs.
If you've got a hunch that a company's stock will be successful, you may only look for supporting arguments during your Google search. If you think social media companies are evil, you may be subconsciously biased in the way you frame your questions, "How evil are social media companies?". If you believe that alcohol is great for your health, you'll only read the studies on how wine has antioxidants, and whiskey kills bacteria.
🖼️ Framing
Narrative is key. How a question is framed affects the perception and outcome.
Bit of a morbid example, but let's say you're considering a surgery for cancer and the doctor says the 1 month survival rate is 95%. Fantastic! That's solid. Now, consider this: there's a 5% mortality rate in the first month. Both arguments are logically the same. But survival is good, and mortality is stressful to think about. Framing matters, and tricky framing can disorient our System 1.
📈 Correlation & Causation
For those who took Statistics 101, here's a reminder: Correlation does not imply causation. Our minds are wired to seek patterns — and once one's spotted, our ego tempts us to rationalize it. Sometimes it's based on logic, other times — pure nonsense.
Some fun examples of correlation without causation (though if you think hard enough you can probably come up with a narrative):
Number of storks and birth rate in Denmark
Number of priests in the USA and alcoholism
🚣🏾 Sunk Cost
Ah, Microeconomics 101. During my first year of college, everyone was talking about sunk cost. Forcing myself to go to a crappy concert because I already paid for the ticket. Putting more money in a poker game because I had already lost (or invested?) a sum of money. Fun times.
The more we invest in something, the less likely we are to to let it go. Sunk costs are past costs that are not recoverable and should not influence future decisions.
⚓ Anchoring
A great tool for manipulating consumers. Anchoring refers to decisions under the influence of an anchor or particular reference point.
Anchoring is used heavily in consumer retail, software sales, and classic negotiation scenarios.
If you see a shirt for $500 and another for $200, you'd likely consider the second one cheaper. In comparing three phone plans: 2GB for $60, 5GB for $80, and Unlimited for $100, you may consider the Unlimited option the best bang for buck. But: Do you even need unlimited? …How much time are you spending on Instagram?
🙋♂️ Availability Bias
Things that come more readily to mind are more representative than is actually the case.
We tend to remember more vivid events such as plane crashes and lottery wins, leading us to overestimate the likelihood of those events occurring. In reality, those are just more graphic, dramatic — and thus, memorable, occurrences.
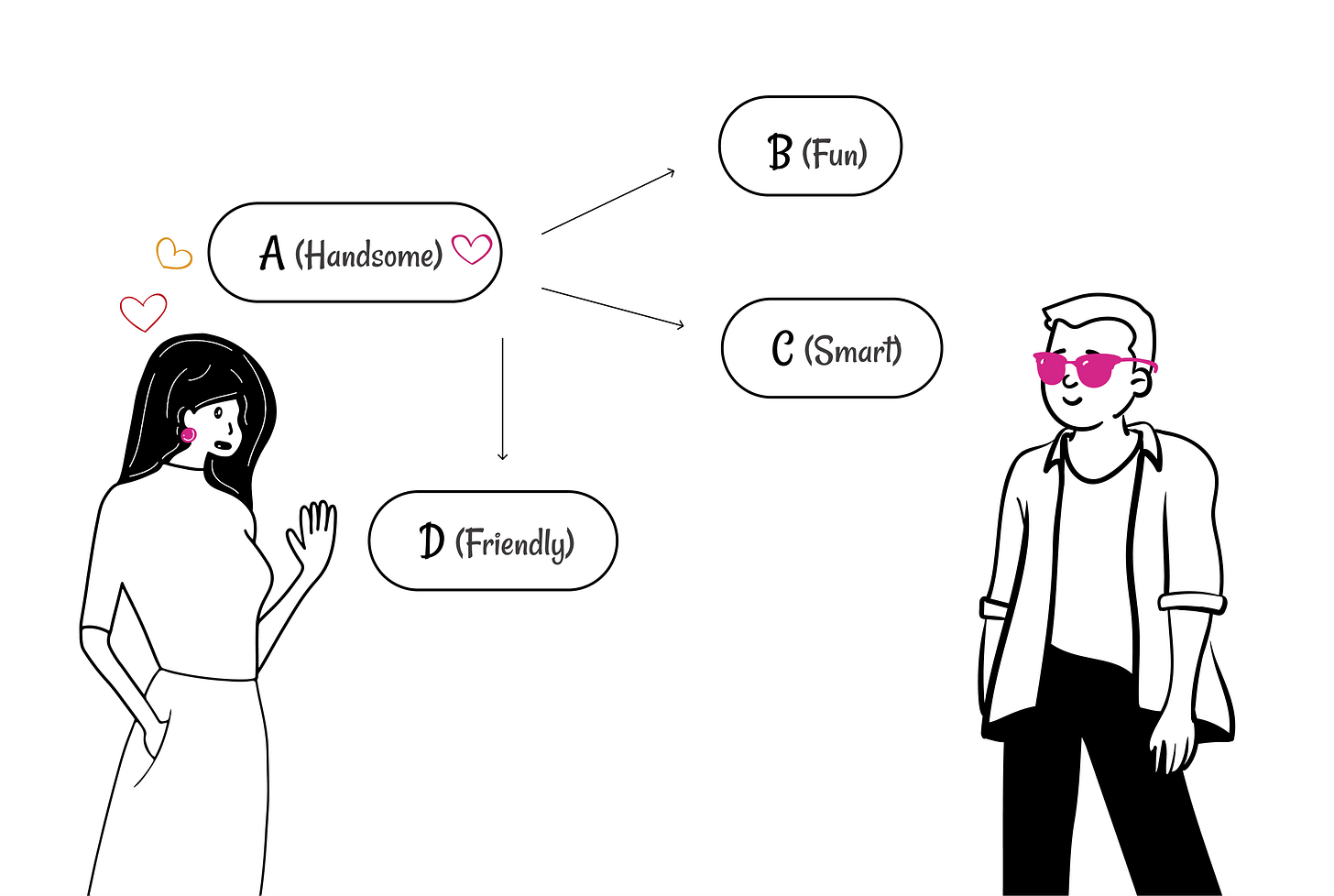
😇 Halo Effect
If we judge a person positively in one respect, we're more likely assume they'll be positive in another. We may assume that a good looking person is also a nice person. Or that a charismatic person is a high performer at work. Perhaps a sharply dressed colleague is a harder worker.
💸 Loss Aversion
Daniel Kahneman received the 2002 Nobel Memorial Prize in Economics for coining this concept. It's the thought that losing something (e.g. money) is twice is powerful as the pleasure of gaining. Folks are more willing to take risks to avoid a loss than to make a gain.
Here's an example:
Would you rather receive $900 with 100% certainty OR receive $1000 with 90% certainty and $0 with 10%?
Would you rather lose $900 with 100% certainty OR lose $1000 with 90% certainty and lose $0 with 10%?
In scenario 1, most people would pick the sure gain (more risk averse). In scenario 2, most people would pick the riskier option (losing $1000 at a 90% chance and nothing at a 10%) chance. Mathematically, both options in scenario 1 and scenario 2 result in the same outcomes of $900 or -$900.
Reducing Bias
As you've realized by now, we're not naturally logical beings (although we sure think we are). Dealing with bias is something folks in all fields — at all levels of seniority — deal with.
Through discussion, reading, and listening, here's how I recommend you can reduce bias.
Develop an awareness of any potential bias that may be clouding your thinking. Awareness is always the first step, and while I've listed eight types of bias here, there are many more. Review different types of bias and visualize them in detail. When you encounter a relevant scenario, acknowledge the bias involved and your self-awareness muscle will develop over time.
Pause and consider: is there any additional information I'm missing? Always seek new information and evidence. Data is king and while we don't always have the luxury of slowing down, we naturally exaggerate the speed of which we need to make a decision, thanks to our hyperactive, anxious brains.
Assess opposing arguments. I used to work with a colleague and friend who played the role of devil's advocate really well (Hey Noah). Healthy debate creates value. And it's good to keep your ego in check by having someone respectfully challenge your point of view. Some companies even practice pre-mortems — brainstorming all the ways a project could fail, prior to launching.
Reframe the problem and invert if needed. By reframing the challenge at hand or decision to be made, you may see the problem differently. I mentioned framing bias above as a negative element. But you can use this as a tool for positive outcomes too. I discussed Inversion as a practical heuristic in March.
Rely on past experience and feedback loops. Have you encountered this problem before in other forms? Experience is the best teacher, though sometimes we tend to forget them. Consider developing a systematic review process to evaluate the quality of your decisions. In most cases, your product is decisions.
Further reading:
Thinking in Bets: Making Smarter Decisions When you Don’t Have All the Facts by Annie Duke
Predictably Irrational: The Hidden Forces That Shape Our Decision by Dr. Dan Ariely
Blink: The Power of Thinking Without Thinking by Malcolm Gladwell
📈 Chart of the week
Australia, New Zealand, Japan, and Switzerland are the most livable cities in the world. According the Economist’s Intelligence unit, these cities rank highest in 30+ qualitative and quantitative factors, spanning stability, healthcare, culture, environment, education, and infrastructure.
I’m fortunate enough to have visited both Osaka and Tokyo many times. I’d highly recommend. Amazing cuisine that suits a variety of palettes. Very scenic and beautiful. And incredible, friendly people.
Appreciation & Support
Thank you for taking the time to read — It took a while to put this together. If this was helpful, I really do appreciate it if you subscribe or share the Twitter thread below.